One of my motivations for starting a blog was Eugenia Cheng’s book The Joy of Abstraction 1. It’s a surprisingly accessible, gentle introduction to category theory, a topic that is usually only taught to graduate students in math. She compiled part of the book using notes from a class that she teaches at the Art Institute of Chicago, which is a testament to the aesthetic appreciation that one can expect to gain of category theory irrespective of their academic background! In this post, I will introduce the main ideas in category theory (as I best understand it) and show that it offers an elegant way of thinking about mathematics.
The Main Idea
The mathematician Tai-Danae Bradley describes category theory as a sort of ‘mad libs’ for mathematics. Mad libs is a game where you have a sentence with a few blank spaces, and depending on what you place in the blank space, you get a different interpretation out of it:
Your [noun] is so [adjective] that it's making me [adjective]!
Mad libs fix the structure of the sentence, but the objects you put in let you extract different interpretations out of it. Try putting in the words blog, boring and sleepy 😕
Category theory lets you do something similar. Every now and then you encounter something in mathematics that makes you go “Hey, this feels a lot like that other thing!” If there were some way to move back and forth between the two universes that have a similar structure, we can apply the insights that we gain in one universe to the other. The following is an example of where I might want to ‘move between mathematical universes with the same structure’:
As an example, consider the statement $\textbf A$ = “Today is Sunday” and $\textbf B$ = “Tomorrow is a Monday.” The statement $\textbf A\Rightarrow \textbf B$ is true, but so is its contrapositive $\neg \textbf B \Rightarrow \neg \textbf A$, i.e., “If tomorrow is not a Monday, then today is not Sunday.”
Now consider the following relationship between sets $A$ and $B$ (not to be confused with the propositions $\textbf A$ and $\textbf B$):
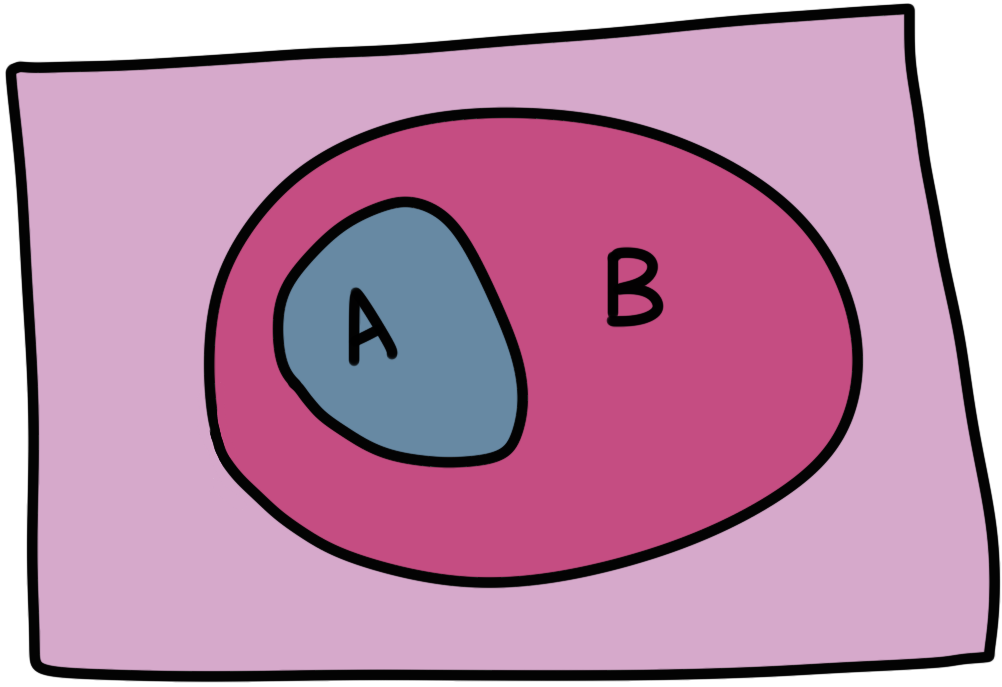
Everything that's outside $B$ is also outside $A$.
Even if these examples are of no interest to you, all we need to note is that we replaced the symbol $\Rightarrow$ (implies) with $\subseteq$ (is a subset of), but the relationship between the corresponding objects looks nearly identical2. As the objects we’re swapping out become more complex, the insights that carry over during the ‘swapping out’ become deeper.
The two different mathematical universes (logic and set theory) consist of objects (statements and sets) as well as relationships between them ($\Rightarrow$ and $\subseteq$). Similarly, a category is something that is made up of objects as well as their relationships to each other (called morphisms), satisfying some additional rules which impart to it its structure.
Categories
The best part of category theory is that it takes a whopping $10$ minutes or so to set up the foundations of it, but it comes with rich insights and new ways of thinking about math. Let’s give the definition of a category.
A category $\mathcal C$ consists of objects and morphisms; the latter are basically arrows from one object in $\mathcal C$ to another. We write $\text{ob}(\mathcal C)$ to refer to the collection of all the objects in $\mathcal C$. Given two objects $X$ and $Y$ in $\text{ob}(\mathcal C)$, we write $\mathcal C(X,Y)$ to denote the collection of all the morphisms (i.e., arrows/relationships) from $X$ to $Y$. Note that (unlike in the above two examples) there may be more than one arrow in $\mathcal C(X,Y)$.
If there is an arrow $f$ from $X$ to $Y$, and an arrow $g$ from $Y$ to $Z$, then we can draw an arrow from $X$ to $Z$ (which represents the path of going from $X$ to $Y$, then to $Z$). We call this specific arrow from $X$ to $Z$ as the composition of $f$ and $g$, denoting it as $g\circ f$. We also say that $f$ and $g$ are composable, since the arrow-head of $f$ touches the tail of $g$.
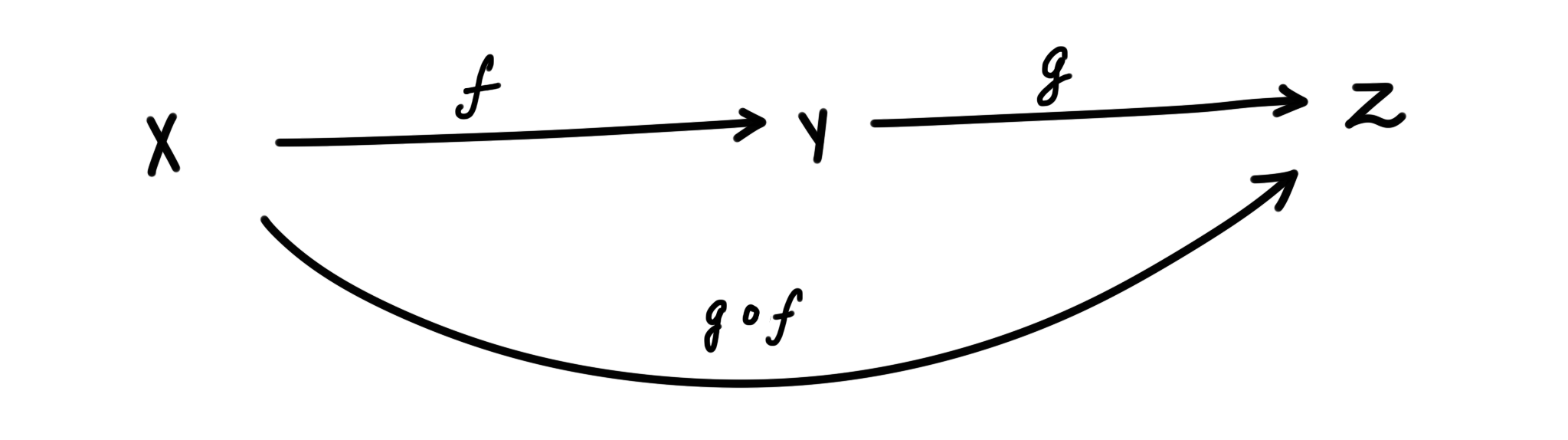
In addition to objects, morphisms, and their compositions, any category has an underlying structure that is imparted to it by the following properties:
- Identities: For every object $X$, there exists a morphism $1_X$ from $X$ to itself, called the identity morphism. Moreover, for any $X$ and $Y$ in $\text{ob} (\mathcal C)$ and $f$ in $\mathcal C(X,Y)$, we must have $f \circ 1_X = f = 1_Y \circ f $. In other words, $1_X$ is like $\text{stay at X}$, and $1_Y$ is like $\text{stay at Y}$.
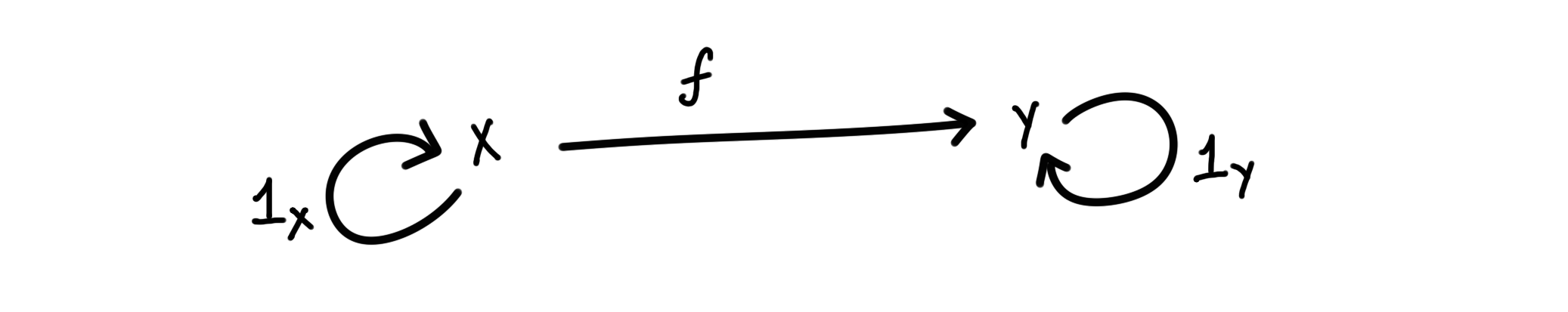
- Associativity: For $f$, $g$ and $h$ in $\mathcal C(W,X)$, $\mathcal C(X,Y)$, and $\mathcal C(Y,Z)$, respectively, we must have $h \circ (g \circ f)$ = ($h \circ g) \circ f$. Visually, the pink arrow in this figure can be obtained in two equivalent ways:
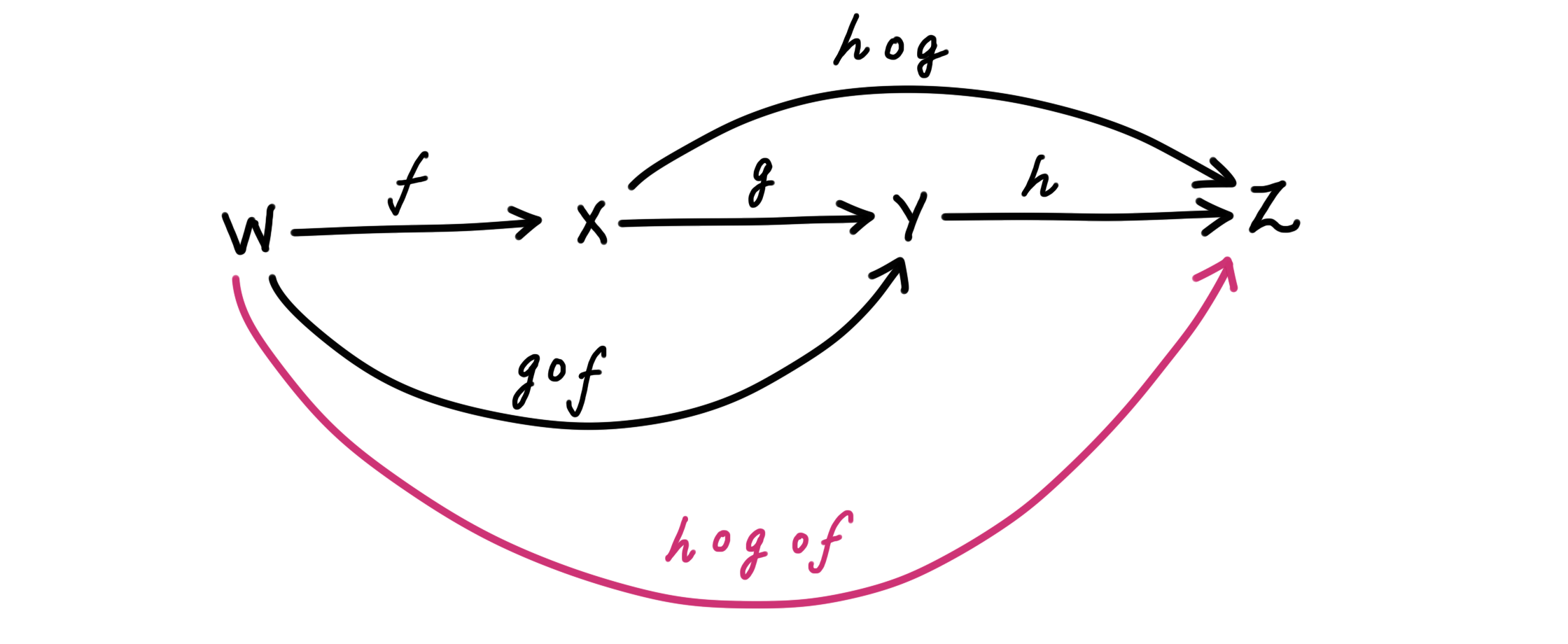
For e.g., if $X$ and $Y$ are vector spaces and $M$ is the linear transformation that takes $X$ to $Y$, then the first bullet point is saying that $ M I_X = M = I_Y M$, where $I_X$ corresponds to the identity matrix of the vector space $X$ (note that $I_X$ and $I_Y$ may have different dimensions as matrices!). Similarly, the second bullet point is just stipulating the associativity of matrix multiplication, which we are so used to that we take it for granted. The order in which we compose arrows (that are composable) does not matter.
In the two examples we gave earlier, logic and sets, we introduced the morphisms $\Rightarrow$ and $\subseteq$, respectively. Since $\textbf A \Rightarrow \textbf A$ and $A\subseteq A$, we do have identity morphisms (arrows from the object to itself) at each object. Similarly, if the objects are numbers, then $\leq$ is another morphism that serves both as an identity as well as a relationship between two distinct numbers. At the same time, $<$ would not work as an identity morphism, as it is not true that a number is $<$ itself.
Observe that we are in the business of ‘swapping out’ morphisms and not just objects.
The Category of Sets
We could define a category $\mathcal C$ consisting of sets (as its objects) in many different ways, depending on what sort of relationships (morphisms) we want to represent between them. However, the category of sets refers to one particular type of category. It is the category $\mathcal C$ where $\text{ob}(\mathcal C)$ are sets and $\mathcal C(X, Y)$ is the collection of all the functions from sets $X$ to $Y$. A function $f$ in $\mathcal C(X, Y)$ assigns to each element in $X$ an element in $Y$.
Now I’ll demonstrate why this representation of sets is cleaner than the way we usually think about sets. Recall that a function $f:X\rightarrow Y$ is injective or ‘one-one’ if for all $x_1,x_2 \in X, f(x_1)=f(x_2) \Rightarrow x_1 = x_2$. In other words, two different elements cannot map to the same element. The function $f$ is called surjective or ‘onto’ if for every $y\in Y$, there exists some $x\in X$ such that $f(x)=y$. In other words, the image of $X$ under the operation $f$ gives all of $Y$, and not just some part of $Y$. (The arrows in the following illustration are NOT supposed to be morphisms! Let’s emphasize that these are illustrations rather than diagrams.)
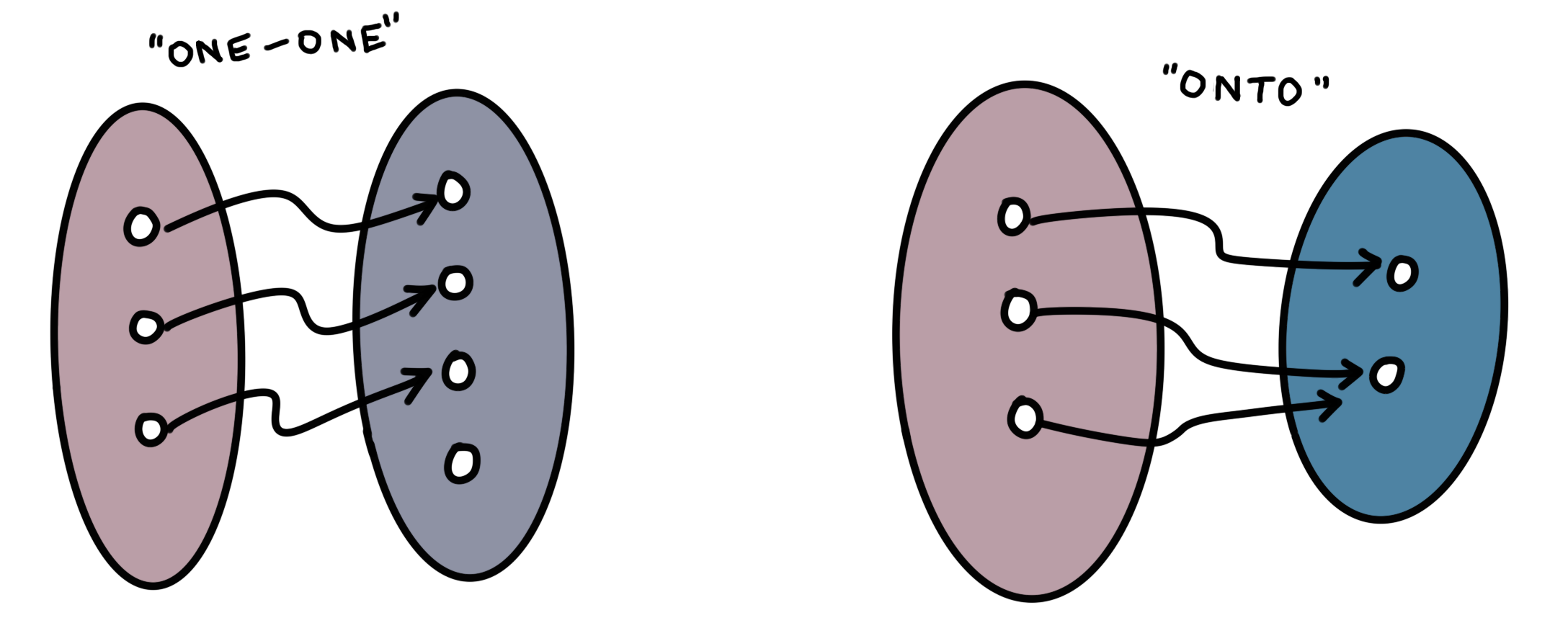
Now I don’t know about you, but these definitions look pretty asymmetrical to me. If I’d never seen them before, I would guess that they are talking about two completely different concepts. The two concepts are united by the fact that if $f$ is both injective and surjective, then it is invertible, i.e., there exists some function $g: Y\rightarrow X$ such that $g \circ f = 1_X$ and $f\circ g = 1_Y$. In this case, $f$ is said to be bijective, and $g$ is called the inverse of $f$.

As an example, let $X$ be a set of people and $Y$ be some tasks or missions. $f$ is the assignment of people in $X$ to tasks in $Y$. The inverse function $g$ can then be thought of like ‘holding people accountable for their tasks’. If a task or a mission goes badly, we want the inverse function $g$ to tell us exactly who to hold responsible for its failure. If $f$ is not injective, either of two people who worked on the same task may be to blame. If $f$ is not surjective, it means that we don’t have anyone to blame for one of the tasks, because apparently no one was even assigned that task. These are the situations in which the inverse function $g$ fails to exist.
We just saw that invertible functions between sets has a purely categorical definition, namely the existence of a ‘reverse’ morphism from $Y$ to $X$ satisfying some properties. We could extend this definition to define invertible morphisms in any category. At the same time, we could ask if there is a purely categorical definition of injective and surjective functions.
Monics and Epics
In any category $\mathcal C$ with objects $X$ and $Y$, a morphism $f$ in $\mathcal C(X, Y)$ is said to be a monomorphism or a monic between $X$ and $Y$ if for all objects $Z$ and morphisms $g_1$ and $g_2$ in $\mathcal C(Z, X)$,
\[ f \circ g_1 = f\circ g_2 \quad \Rightarrow \quad g_1 = g_2 \]
In any category $\mathcal C$ with objects $X$ and $Y$, a morphism $f$ in $\mathcal C(X, Y)$ is said to be an epimorphism or an epic 😎 between $X$ and $Y$ if for all objects $Z$ and morphisms $g_1$ and $g_2$ in $\mathcal C(Y, Z)$,
\[ g_1 \circ f = g_2 \circ f \quad\Rightarrow \quad g_1 = g_2 \]
In the category of sets, the monomorphisms and epimorphisms are precisely the injective and surjective functions, respectively. Now these definitions look so symmetric that they almost seem wrong. So why is it that they are equivalent definitions for injectivity and surjectivity, respectively? To begin with, why is a monomorphism, as defined above, necessarily an injective function (and vice versa)?3
1. Monics are Injective Functions
The trick is to think of a monomorphism $f:X\rightarrow Y$ as a re-labeling of the elements of $X$. Suppose $X$ is a set of people and $Y$ is a set of (distinct) names, then let $f$ be the operation of assigning each person a name. $f$ is injective if each person gets a distinct name (no two people have the same name). In that case, if I give you a list of names, you know exactly which list of people I picked. In the figure, the purple arrows are the monomorphism (assignment of distinct names):
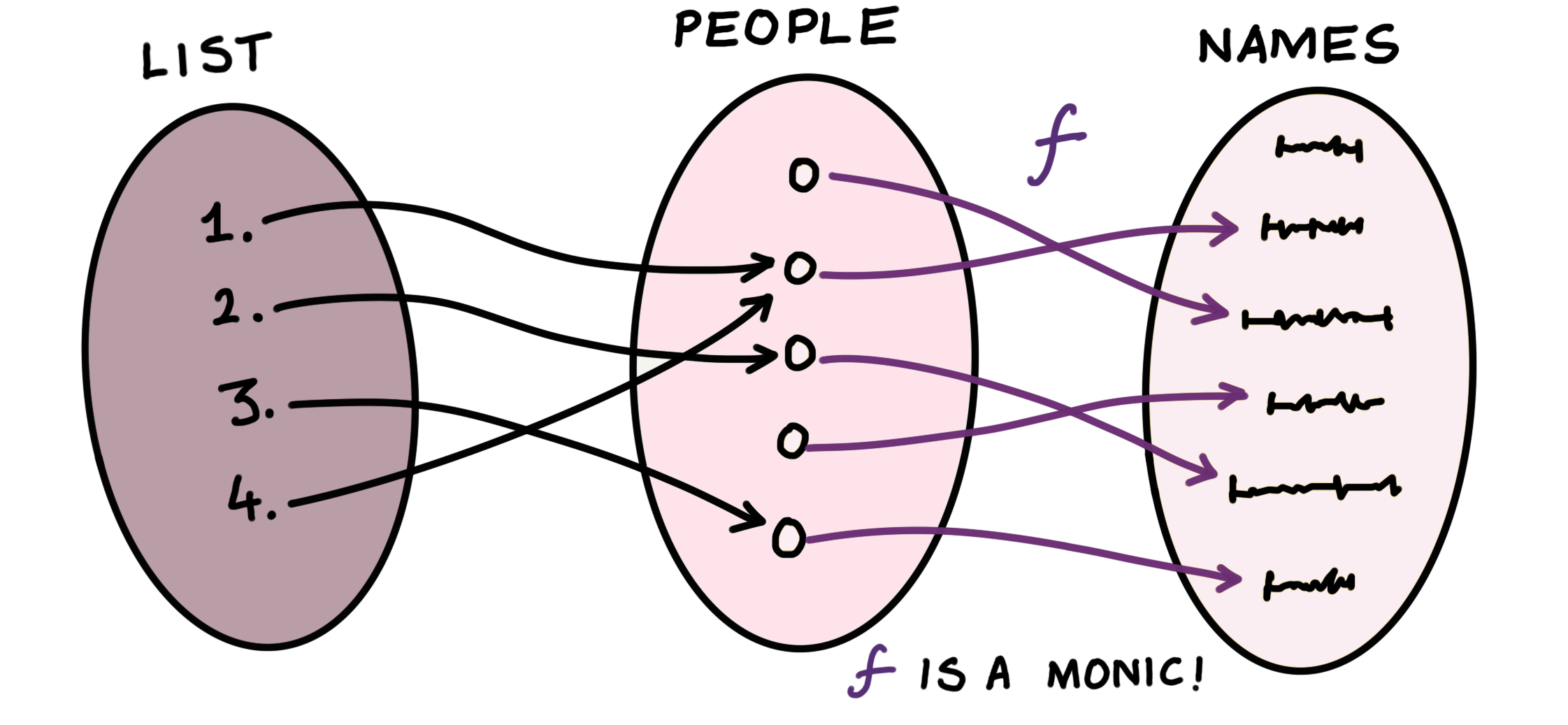
$f$ would not be a monomorphism if two people were given the same name, say, John, i.e., two of the purple lines go into the same name. In that case, I could have picked either John (corresponding to two different lists of people, $g_1$ and $g_2$) but produced the same list of names ($f \circ g_1 = f \circ g_2$), and you would have no way of telling which list of people you were looking at since you do not know which John I picked. You would instead point a finger at me and accuse me of being ‘ambiguous’.
Succintly, $f$ remembers which elements went to which elements. It does not forget that there are $n$ distinct people by assigning two or more of them the same name.
2. Epics are Surjective Functions
Finally, let’s see why the definition of epimorphisms of sets works as the definition for surjectivity. This is perhaps more difficult to see, because it looks so different from the set-theoretic definition of surjectivity. Let’s take this post to a full circle and invoke the contrapositive of the definition for an epic, which says that an epimorphism or an epic is, equivalently, a morphism $f$ in $\mathcal C(X, Y)$ such that for all objects $Z$ and morphisms $g_1$ and $g_2$ in $\mathcal C(Y, Z)$,
\[ g_1 \neq g_2 \quad\Rightarrow \quad g_1 \circ f \neq g_2 \circ f \]
This means that pre-composing $g_1$ and $g_2$ with $f$ retains the ability to distinguish $g_1$ and $g_2$. Suppose $f$ weren’t surjective, then we may no longer be able to distinguish $g_1$ and $g_2$ because $f$ is not even ’looking at’ one of the elements, which may be crucial to distinguishing $g_1$ and $g_2$:
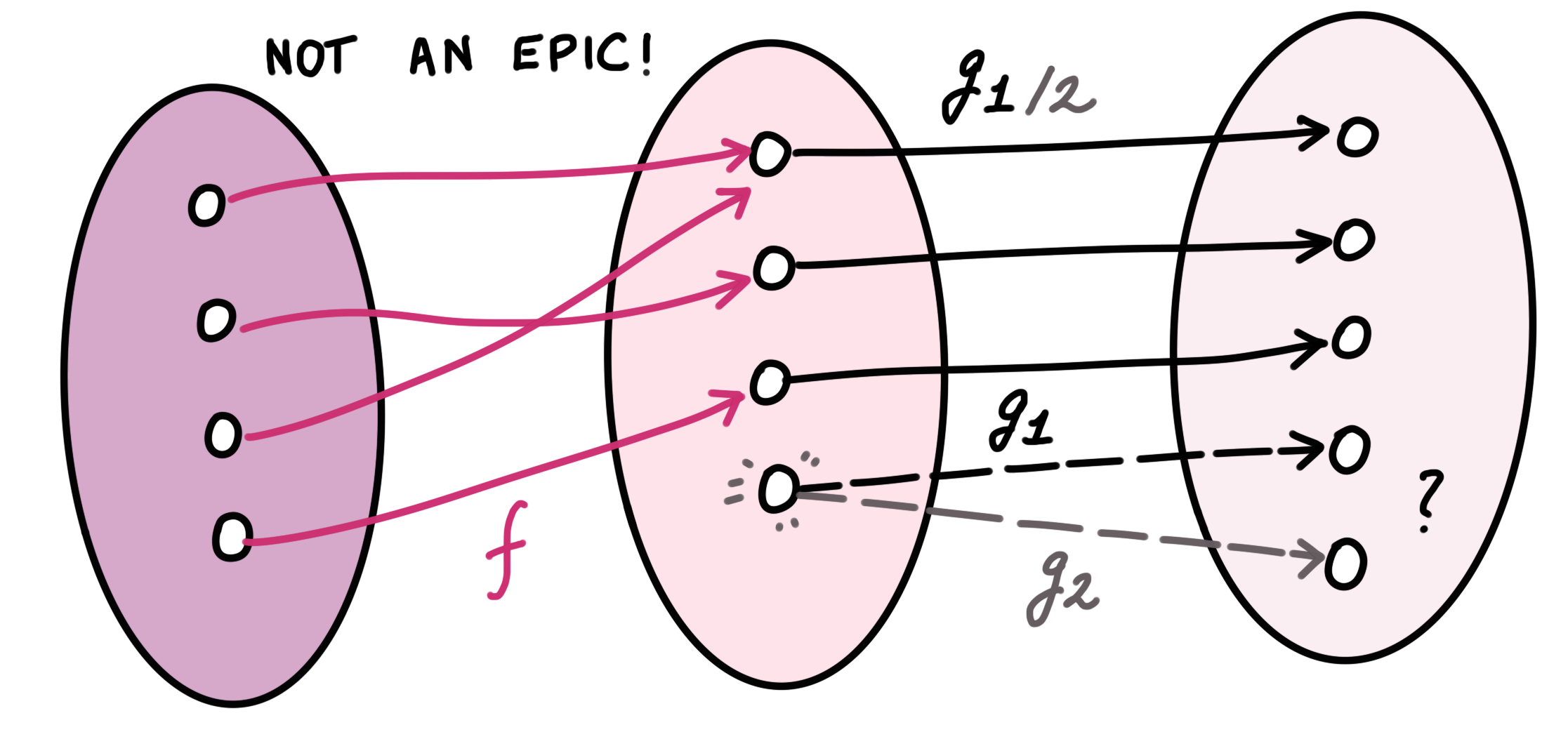
Similarly, the definition of monics (which are the injective functions) was really saying that post-composing with $f$ retains the ability to distinguish two morphisms $g_1$ and $g_2$, because in that case $f$ was just a re-naming of the objects.
Thinking Categorically
Two days after I first published this post, two of my favorite math communicators made a podcast episode about category theory. Eugenia Cheng talks to Steven Strogatz about why she finds joy in thinking categorically, i.e., approaching these types of math concepts from a category theory standpoint.
What we showed above was that some concepts in math might be a bit messy or aesthetically lacking due to how they’re set up. This messiness also prevents us from generalizing ideas like injectivity and surjectivity to other fields in math, because they’re too deeply rooted in the language of set theory. Category theory allows us to squint at mathematical objects in just the right way, until we’ve ‘blurred out’ the messiness, focusing our attention only on the thing that really matters: structure! As a bonus, we get to apply our insights to all of the other mathematical fields that have analogous properties, and therefore similar (or identical) structures. I would argue that this is a joyful way of learning mathematics. One where all of mathematics is yielding itself to you, simultaneously.
-
At the time of me writing this post, there is an ongoing book club for The Joy of Abstraction being hosted by its author. ↩︎
-
Either statement is a consequence of duality in category theory. Duality manifests again on my blog when I talk about differential forms . ↩︎
-
We just showed one direction of each of these equivalences, at best. The main goal is to get an intuition for why the two definitions of injectivity and surjectivity may be equivalent! ↩︎