The Incompleteness Theorems

In my earlier post I suggested that there is no objective notion of logical truth, that whether a statement is ’true’ can depend on the system of truth that one is operating in. Here we will develop that argument further using the concept of axiomatic systems. This is a long one, but I’m excited to talk about it!

Axiomatic Systems

An axiomatization is an assignment of rules (axioms) such as “one plus one equals two,” making up an axiomatic system or a formal system. If you happen to be within that formal system, then you must follow all of the assigned rules. The choice of axioms dictates the degree of expressiveness that one has within the formal system. For instance, North Korea has a small number of state-approved haircuts that everyone must choose from, which does not sound like a very expressive system.

Similarly, in pre-elementary school mathematics you are introduced to the natural numbers: $0$, $1$, $2$, $3\dots$ You can add one natural number to another, but don’t you dare subtract them! Once we allow subtraction, we are able to express negative numbers such as -$5$. Then comes multiplication, which doesn’t seem to introduce any new numbers. By middle school, we are allowed the use of division, which grants us a greater degree of expression. We are able to concoct fantastic things such as $2.25$.

Formal systems which can (to varying extents) characterize the natural numbers include the Presburger arithmetic, Peano arithmetic, and the Zermelo theory. These are all formal systems named after their respective conceivers. There is no single canonical formal system for describing numbers. In fact, different systems capture different properties about the numbers, and we may be interested in exploring these properties and the ensuing mathematical structure. In the $1920$s, Zermelo’s system was extended (similar to how we extended the integers to the rationals, above) to the Zermelo-Fraenkel (ZF) set theory , often touted as being the foundation of modern mathematics , as it captures just about every mathematical concept that we come across in school. To see just how pedantic mathematicians are (I mean that in the most endearing sense), a key addition to the Zermelo-Fraenkel theory over Zermelo’s was that we could now count not just to infinity, but beyond . Of course, 21^st century mathematicians are interested in adding more axioms to this system so that we can find new infinities in between the existing infinities ¹. It seems as if somebody should stop them from taking this bit any further.

I can’t speak for whether we invented numbers, but we definitely made up the rules for how they behave. I guess you could argue that we did make up numbers, but only so far as to effectively capture the essence and structure of our perceived reality. The natural numbers described by each of the above formal systems works precisely like counting does, $1$ plus $2$ makes a $3$. Maybe there is such a thing as a ’number’ that just exists out there, but the numbers we use in our everyday math is the version that was invented by humans. It’s Zermelo and Fraenkel’s best approximation of what being a number entails. Like the cavemen in Plato’s allegory, we can trace over shadows on a wall, even if we can’t see or touch the objects casting these shadows.

Mathematics is certainly not just the study of numbers, though. It can be regarded as the study of patterns and structure instead. One begins this process by carefully choosing the axioms so as to best represent the structure that is to be studied, then further structure emerges through the logical inferences that are made about these axioms. Entire mathematical fields can be founded on axioms (i.e., we don’t always have to start by describing numbers). For doing probability we could use the Kolmogorov axioms , for geometry there’s Euclid’s axioms, for group theory we have group axioms, and so on.

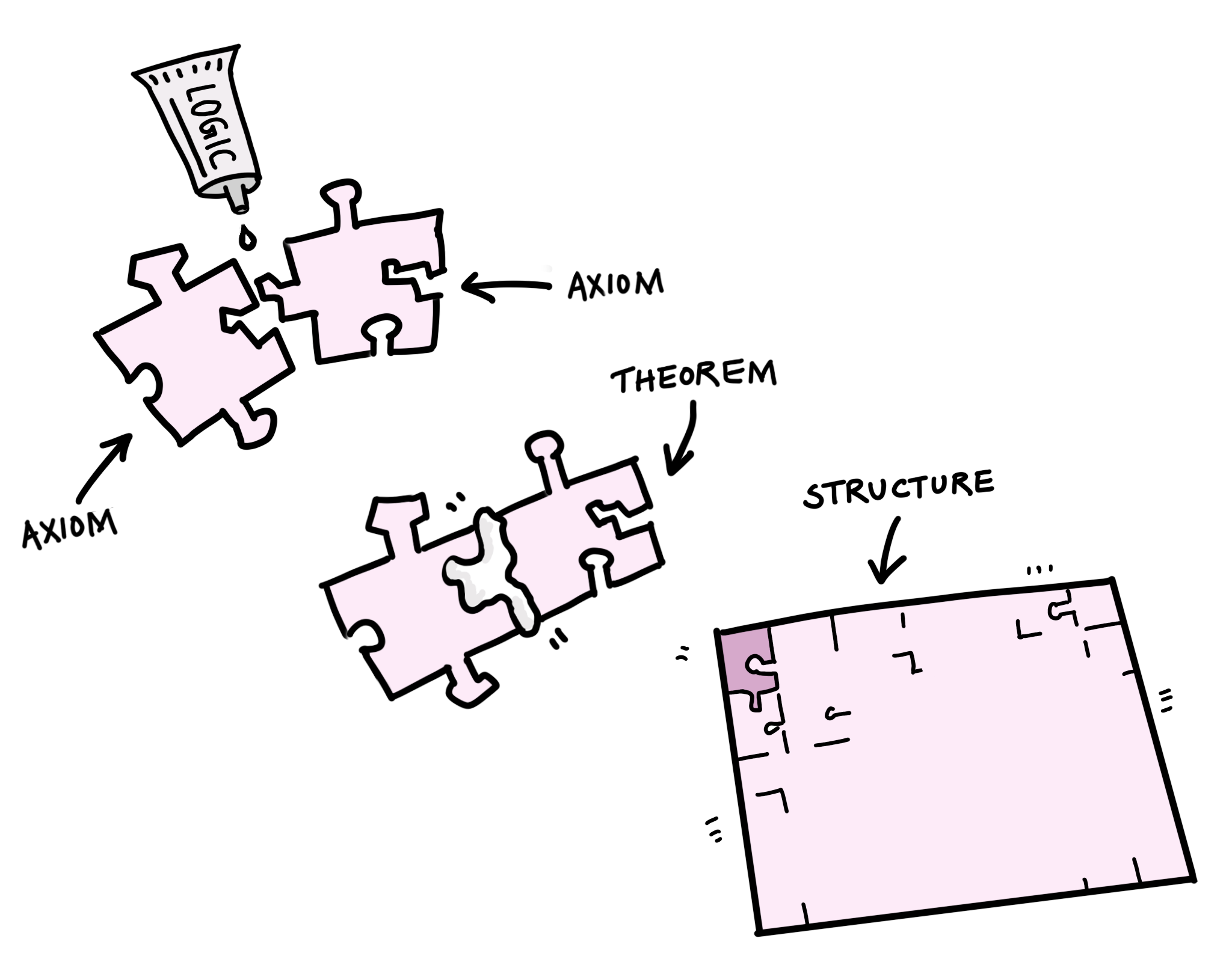
There is a school of thought within mathematics called logicism , which believes that all of mathematics was founded on logic, logical inference was the glue that held axioms together to form theorems. More specifically, they believed that any mathematical truth could be proved using the one-two punch of axioms and logical inference. The mathematician David Hilbert was at the helm of this movement in the $1920$s. Hilbert is perhaps best known for posing a series of unsolved problems in mathematics, most of which were conjectures that mathematicians felt were true, but had neither been able to prove nor disprove yet. One of these conjectures was that all of mathematics can be founded on logic.

But wait a second, the whole point of this exercise was to figure out how logic could itself be defined. After all, logical inference should itself follow rules, else the formal systems based on them would be kind of messy and all over the place. Well, we could define logic as being a formal system unto itself! The Zermelo-Fraenkel theory (which, recall, is the formal system underlying most of modern mathematics) is built on first-order logic , which is indeed a formal system. First-order logic comes with, in addition to its axioms, its own formal system for logical inference, called zeroth-order logic or propositional logic .

Before we continue, it is worth mentioning that some languages (but not natural languages like English) can be defined as axiomatic systems too, and there are good reasons for why one might want to do this. Formal languages have been used to study linguistic structures. Alfred Tarski (of the Banach-Tarski paradox fame) also attempted to define truth using formal languages, noting that using a formal language one could construct a consistent, fool-proof definition for truth that was free of ambiguity.

Then there are programming languages. Alan Turing introduced the concept of Turing machines (which are axiomatic systems) to study the fundamental limitations of computers, laying the foundation for all of theoretical computer science. Amazingly, he did so in a time when the word computer referred to a human occupation, not an electronic machine. We’ll revisit both Tarski and Turing’s works later in this post.

Choosing the Axioms

Let’s ask the question of how one chooses an axiomatic system. What kind of axioms would we want for our system? Suppose $A$ is an axiom and $\neg A$ is its negation, i.e., the statement ‘$A$ is not true’. Clearly, $A$ and $\neg A$ cannot both be axioms as this gives us a contradictory system. So we have our first requirement:

CONSISTENCY – It should not be possible to prove contradictory statements

We should also have the ability to prove things within an axiomatic system. Proofs (or disproofs) are how we can be certain that something is true (or false). Those unsolved problems that Hilbert posed? Surely, any good axiomatic system will have either a proof or a disproof of each of the conjectures. Anything that is proved, we can call a theorem. If a conjecture gets disproved instead, we can negate it and call that a theorem. That is ideally how we would like to do mathematics.

COMPLETENESS – Anything that we feel is true should be provable

Finally, a characteristic of a useful axiomatic system is that we are able to do something with these axioms. A mathematics based on just $12$ numbers may be sufficient to tell the time, but there are many situations where we would like to count past 12. This leads us to the very subjective stipulation which we call expressiveness.

EXPRESSIVENESS – The axiomatic system should have a variety of objects and relationships that we can, for example, use to describe real-world phenomena

We now have all the background needed to get into the meat of this post.

Gödel’s Incompleteness Theorems

The mathematician Kurt Gödel was able to show, around a 100 years ago, that no axiomatic system can have all three of these qualities. Specifically, he showed that any axiomatic system (that is expressive enough to do basic arithmetic ) is either incomplete or inconsistent. This is called Gödel’s first incompleteness theorem.

Implications in Mathematics

Let’s think about what this means. Suppose we design an axiomatic system that is sufficiently expressive (can do basic computations, like add one thing to another to give two things). Either there are some true statements in it which cannot be proved using the axioms (incompleteness), or there exist contradictory statements in it, each of which can be proved using the axioms (inconsistency). In fact, the latter case, inconsistency, is far worse, and pretty much a deal-breaker. A single contradiction can suspend all credibility of an axiomatic system, because in a contradictory axiomatic system one can prove anything . That’s bad! We don’t want to have one mathematician prove that $2$ plus $2$ equals $5$, another prove that it doesn’t, and have no grounds for deciding who’s right. So it’s looking like we’d rather mathematics be incomplete (i.e., missing some things) than inconsistent (i.e., self-contradictory).

It turned out that at least one of Hilbert’s unsolved problems could neither be proved nor disproved, namely the continuum hypothesis (which conjectured that there is no set that is bigger than the integers and smaller than the real numbers). There was absolutely nothing that the Zermelo-Fraenkel ($ZF$) system could say definitively about this conjecture. So then what do we do with the continuum hypothesis ($CH$)? Does it not have a place in mathematics? Well, we could assume $CH$ is true and adopt it as a new axiom. We could also assume that it is false (which we write as ‘$\neg CH$’) and adopt that as an axiom instead. Adding an axiom like this comes with its consequences, though. For instance, $ZF + CH$ implies that the infamous axiom of choice holds, which in turn leads to the Banach-Tarski paradox . Put simply, this means that geometry can have non-intuitive (‘weird’) properties in $ZF + CH$. So we want to double-check whether we indeed want geometry to behave in this way, before adding $CH$ (or $\neg CH$) as an axiom to $ZF$.

Mathematicians are able to show that adding $CH$ at least does not make $ZF$ inconsistent, but that’s another possibility we should consider before adding new axioms. Given a choice, we’d rather be incomplete than inconsistent.

Reasons for Incompleteness

There are axiomatic systems which are indeed consistent and complete, and first-order logic is one of them! (This is the content of the lesser known Gödel’s completeness theorem.) The incompleteness theorems require us to first qualify how expressive a system is, before we can say anything about its incompleteness. So let’s now look at when and why a given axiomatic system, be it language, logic, or mathematics, comes under the purview of the incompleteness theorems.

Infinity / Recursion: Observe that, if an axiomatic system has only finitely many statements in it, we can just enumerate through all of its statements and check whether they’re true. Sort of like a brute force proof. A brute force proof in a system with infinitely many ’things’ in it either may or may not terminate (see the four color theorem and the Riemann hypothesis , respectively, for examples of either case.)

Recall that Alan Turing’s work involved the study of programming languages, or rather, the computer algorithms that can be written using them. He showed that no computer program can decide (determine with certainty) whether another computer program ‘halts’, i.e., terminates, as opposed to getting stuck in an infinite loop. This is called the halting problem, and it is said to be undecidable. Here, undecidable only means that there is no effective algorithm to solve the halting problem. Similarly, Gödel’s theorem says nothing about the (non-)existence of infinitely long proofs. It just says that there are statements that do not have finite proofs, but the word finite is typically omitted while stating the incompleteness theorems. (At this point, I would implore the reader who is familiar with Cauchy’s completeness in metric spaces to compare the two uses of the term ‘completeness’ 😃)

It seems like it is necessary and sufficient for an axiomatic system to have some notion of ‘infinitely many things’ in it for Gödel’s theorems to apply. But this isn’t quite the case either. Robinson arithmetic is an incomplete axiomatic system that can be generated using finitely many axioms. On the other hand, Tarski's theory of real closed fields is a complete and decidable axiomatic system that characterizes the infinitely large set of real numbers².

As a segue, consider the following block of (Python) code, which prints infinitely long strings of letters:

1
2
3

def recursive_function(x):
    print(x)
    recursive_function(x)

The function above takes some input x and uses what programmers call ‘self-reference’ to print the object x infinitely many times on the screen, indicating that self-reference has the potential to generate infinitely many things. This is a hint at the fact that self-reference, and not infinitude, may be the deeper reason for incompleteness.

Self-Reference: A universal feature of axiomatic systems where Gödel-like incompleteness theorems do apply is that these systems are capable of self-reference. Self-reference leads to what we call in common parlance paradoxes. A well-known example of a paradox arising from self-reference is “This statement is false”; we can’t assign a truth value to this statement without arriving at a contradiction, exactly as in Gödel’s theorem. Another well-known paradox from mathematics (which is of historical significance) is Russel’s paradox, which asks whether the set that contains all the other sets contains itself. Russel’s paradox showed that ’naive set theory’ (one in which you can even posit the existence of such a ‘set of all sets’) is inconsistent.

The ‘ Barber paradox ’ is a more prosaic way of asking the same question: There is a village that has only one barber, who shaves those (and only those) who do not shave themselves. Does the barber shave himself?³

A lot of Gödel-like theorems use proof by contradiction , where the contradiction arises from self-reference. Turing’s proof of the undecidability of the halting problem involves giving a computer program a version of itself as the input. (It’s a very accessible proof, so you could watch this video if you’re curious!)

The Second Incompleteness Theorem

Okay, so many our axiomatic systems are incomplete, including mathematics. That might be a good thing, right? At least they aren’t inconsistent? Well, the second of Gödel’s incompleteness theorems states that a sufficiently expressive consistent system cannot prove its own consistency! As we already know that the Zermelo-Fraenkel theory is incomplete (because of the unprovability of $CH$), it is guaranteed to have some unprovable statements. One of these unprovable statements is that of its own consistency.

Similarly, recall how Tarski tried to define truth using axiomatic systems, such that the definition of truth varies based on the axiomatic system we’re interested in. In the last post, I suggested that truth is kind of like logical consistency. There is indeed a version of the second incompleteness theorem that swaps consistency out for truth. Tarki’s undefinability theorem says that the concept of truth in a formal system cannot be defined within that system. Tarski’s proof of the undefinability theorem mostly relies on self-reference, rather than on recursion as many other Gödel-like proofs do. It is also about formal systems in general, and not about mathematics. Owing to this fundamentality of Tarski’s theorem, the mathematician Raymond Smullyan showed in $1957$ that Gödel’s incompleteness theorems can be applied to many more formal systems than was believed in Gödel’s time. For these reasons, Smullyan also espouses that Tarski’s work should get much of the attention that Gödel’s does.

It seems like the study of consistency (or provability, truth, etc.) should itself be privy to the problem of self-reference, since we say that a formal system is unable to prove its own consistency. For that matter, the second incompleteness theorem is phrased a bit peculiarly; it doesn’t preclude the possibility that one formal system can prove the consistency of another.

Transcending Language using Metalanguage

As opposed to proofs in a formal system, proofs about a formal system can be expressed in a metalogic or a metalanguage. The metalanguage sits ‘above’ the formal system it is looking at, called the object language, in the sense that it is often more ‘powerful’ or expressive than the object language, and assumes the authority to state and prove theorems about the object language. Proofs about (in)consistency, (in)completeness, (un)decidability, and (un)provability are often stated in a metalogic/metalanguage. Similarly, Tarski’s definition of truth in a language (which is in this case the object language) was stated in a metalanguage, and his undefinability theorem showed that the metalanguage and its object language cannot coincide. As in the case of the incompleteness theorems, all of this only holds unless the object language was not very expressive to begin with. If the language is such that self-reference and/or basic arithmetic are not within its expressive capabilities, then it is indeed possible that it could serve as its own metalanguage, and/or that it is both complete and consistent.

Natural Languages

Natural languages are expressive by design, that’s their whole point. They encompass everything that we would want to talk to each other about. This includes a multitude of axiomatic systems, spanning formal language, logic, and mathematics. Since linguists, logicians, and mathematicians talk to each other in natural languages like English, natural languages should necessarily operate as metalanguages. If there were such a thing as a ‘formal natural language’, it would seem that Gödel’s theorems must apply to it, by virtue of its expressiveness. But in contrast to axiomatic systems of mathematics, we’d probably want a formal natural language to be complete rather than consistent.

If you went to an English-speaking school, you were probably taught the semantics and grammatical constructs of the English language in English. Mathematicians are able to state Gödel’s theorems in English. Computer programmers use English to write pseudo-code. A natural language such as English has some element of completeness in the sense that we want it to do everything. If it weren’t complete, we’d just want a metalanguage ‘above’ it to fill in the holes, and so on. For example, a non-native English speaker may instinctively switch to their native language when they’re trying to express something complex, something they may not have the vocabulary for in English. It is even possible that they went to a school where English (the object language) was taught to them in their native language.

This is similar to how we added $CH$ to $ZF$ earlier to ‘complete’ it in some sense, but we cautioned that it comes at the risk of making the more powerful language, $ZF+CH$, to be inconsistent. In the case of natural languages, we embrace this potential inconsistency as being the trade-off for completeness.

Before we close, I should do my due diligence and note that, while formal languages can be used to discuss natural languages, the latter fall under the category of informal languages and may not have a definable notion of truth. In fact, Tarski explicitly warned against the extension of his ideas to natural languages. Tarski's critics also stress on the distinction between mathematical truth and metaphysical truth, which should not be conflated with each other. Nonetheless, one could argue that the mathematical (or rather, the axiomatic) approach to defining truth is as clean and air-tight a characterization of truth as we can hope to achieve. We just need to bear in mind that we aren’t here to establish a singular meaning for the word truth, but to appreciate the intricacies involved in defining truth and logic. The self-reference in trying to arrive at the true definition of truth shall not be lost on us.