The title is a quote from this math podcast . I mentioned in the last post that Euclidean geometry arises as a special case of the geometry of inner product spaces. And yet, the only spaces that are ’tangible’ to us humans are the $1$, $2$, and $3$ dimensional Euclidean spaces. No other inner product spaces feel nearly as intuitive.
In this post I’m showing how the Pythagoras theorem is a special case of a more general feature of inner product spaces. Contents of the last post are pre-requisites for this one.
The Parallelogram Law
Let $x$ and $y$ be two vectors in a normed vector space that we are interested in. Recall that the existence of an inner product $\langle x, y\rangle$ implies the existence of a corresponding norm, $\lVert x\rVert = \sqrt{\langle x, x\rangle}$. But the converse direction is not always true. When it is true, is precisely when the normed vector space obeys the parallelogram law; for all vectors $x$ and $y$,
\[2\|x\|^2 + 2\|y\|^2 = \|x+y\|^2 + \|x-y\|^2 \]
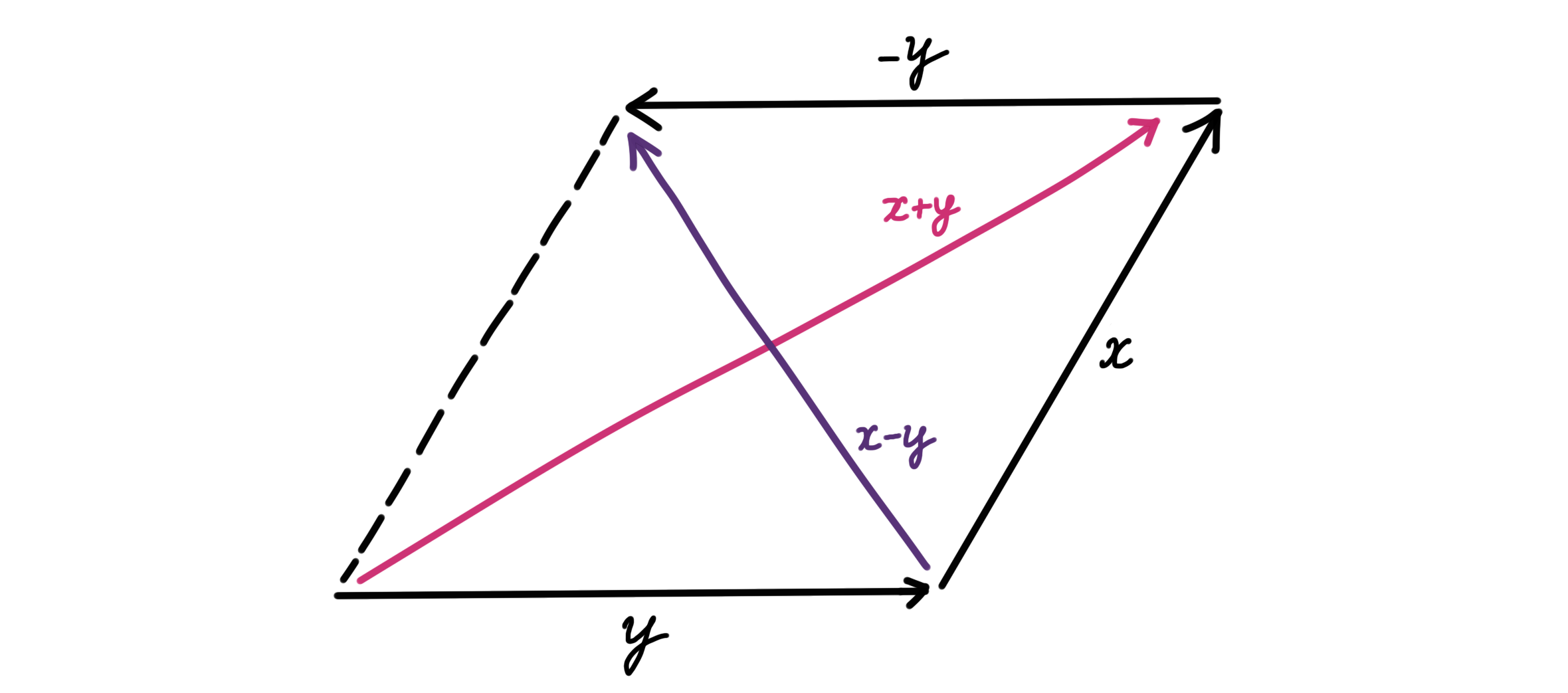
The name of this law comes from the special case of $\mathbb R^2$ shown above, where it is a relationship between the side lengths and diagonals of a parallelogram. Notably, if $\lVert x+y \rVert=\lVert x-y \rVert$, i.e., the parallelogram is a rectangle, then we recover the Pythagoras theorem. Thus, the Pythagoras theorem is a corollary (i.e., a by product) of the fact that $\mathbb R^2$ equipped with the Euclidean norm $\lVert{}\cdot{}\rVert_2$ satisfies the parallelogram law.
Next, let’s see why the validity of the parallelogram law coincides with the existence of an inner product.
Symmetric Bilinear Forms
A symmetric bilinear form is a map $\phi(x,y)$ that takes two vectors $x$ and $y$ of a vector space and gives a real number1, much like an inner product or a metric does. A symmetric bilinear form is symmetric
\[ \phi(x, y) = \phi(y,x) \]
and bilinear
\[ \phi(x+y, z+w) = \phi(x,z) + \phi(x,w) + \phi(y,z) + \phi(y,w) \]
which means that it is linear in either argument. As a part of what we require of an inner product in a real vector space, they must be positive-definite symmetric bilinear forms. Positive definite means that $\phi(x,x)\geq 0$ and $\phi(x,x)=0$ $\Leftrightarrow$ $x=0$.
Now, if we set $z=x$ and $w=y$ in the above expression, and using the positive-definite, symmetric, and bilinear properties of inner products, we get
\[ \langle x+y, x+y \rangle = \langle x,x \rangle + \langle x,y \rangle + \langle y,x \rangle + \langle y,y \rangle \] \[ \| x+y\|^2 = \| x \|^2 + 2 \langle x,y \rangle + \| y\|^2 \]
where we used the notation, $\lVert x\rVert = \sqrt{\langle x, x\rangle}$. As $(-y)$ is also an element of our vector space, we can repeat the same steps to get
\[ \| x-y\|^2 = \| x \|^2 - 2 \langle x,y \rangle + \| y\|^2 \]
The sum of the last two equations is the parallelogram law, whereas subtracting the second equation from the first gives us
\[ \langle x,y \rangle = \frac{\|x+y\|^2 - \|x-y\|^2}{4} \]
Observe that we can use the preceding equation as a definition for the inner product in terms of the underlying norm. Thus, normed vector spaces satisfying the parallelogram law have a unique inner product, which is defined as above. What remains to be shown is that this definition of an inner product using a norm, combined with the parallelogram law (which our norm supposedly satisfies), indeed satisfies all of the requirements that the inner product should .
Special Cases
Suppose the normed space we were working with was $\mathbb R^n$ with the $2$-norm, $\lVert{}\cdot{}\rVert_2$, then as one would expect, the unique inner product we get is the dot product for finite-dimensional vectors $x$ and $y$, which we usually write as $x^Ty$ or $x\cdot y$ in place of the more general notation of $\langle x, y \rangle$. Other $p$-norms do not satisfy the parallelogram law, and hence do not have an associated inner product.
As we saw, specializing the underlying vector space to $\mathbb R^2$ makes the parallelogram law a relationship between the sides and diagonals of a parallelogram. Further specializing to the case where $x$ and $y$ make an angle of $90^\circ$ between each other, i.e., $\langle x,y\rangle = 0$, yields the Pythagoras theorem.
Finally, in $\mathbb R$, the law takes its most plausible form:
\[ (x+y)^2 + (x-y)^2 = 2x^2 + 2y^2 \]
Update: Someone on Mathstodon pointed out to me that what the parallelogram law is really saying is that the norm-squared function $f(x)=\lVert x\rVert^2$ is a degree $2$ polynomial. Let’s explore this real quick.
Notice that a degree $2$ polynomial is characterized by the fact that its second derivative is constant everywhere. Suppose, this constant (which is the Hessian) is $c\cdot\bold I$, where $c$ is some number and $\bold I$ is the identity matrix. Let’s take the Taylor series expansion of $f$ at $x$, sticking to the Euclidean space $\mathbb R^n$ for simplicity.
\[ f(x+y) = f(x) + f'(x)^T y + \frac{1}{2} y^Tf''(x)y \] \[ \qquad \ = f(x) + f'(x)^T y + \frac{c}{2} f(y) \]
Similarly,
\[ f(x-y) = f(x) - f'(x)^T y + \frac{c}{2} f(y) \]
Adding these,
\[ f(x+y) + f(x-y) = 2 f(x) + c f(y) \]
Naturally, we set $c=2$. Thus, we could potentially simplify the parallelogram law to: The norm-squared function is a polynomial of degree $2$, which sounds more fundamental and less arbitrary than the parallelogram law to me, let alone the Pythagoras theorem. But we need to do more work to generalize this math to hold outside of Euclidean spaces. Someone more knowledgeable than me in differential geometry should explore the connection between inner products and metric tensors on Riemannian manifolds !